
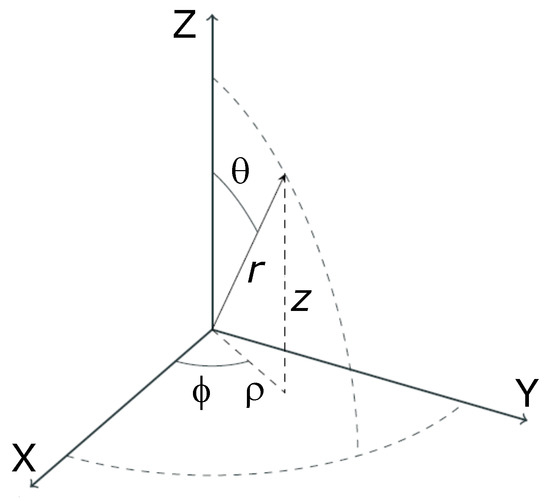
Therefore, it can be seen from the former equation, that when a certain bending moment M is applied to a beam cross-section, the developed curvature is reversely proportional to the moment of inertia I. The base of the 3D rectangular prism above is a rectangle that gives it two. Where Ixy is the product of inertia, relative to centroidal axes x,y, and Ixy' is the product of inertia, relative to axes that are parallel to centroidal x,y ones, having offsets from them d_. A three-dimensional space (3D) has three dimensions, such as length, width. The following diagram shows what it looks like visually: Golden rectangles have been used throughout history in architecture, art, and other areas, both intentionally. Where I' is the moment of inertia in respect to an arbitrary axis, I the moment of inertia in respect to a centroidal axis, parallel to the first one, d the distance between the two parallel axes and A the area of the shape (=bh in case of a rectangle).įor the product of inertia Ixy, the parallel axes theorem takes a similar form: A golden rectangle is a rectangle whose length to width ratio equal to the golden ratio,, which has a value of or approximately 1.618, assuming the length is the larger value. Our technique provides an easy to use solution that is. The so-called Parallel Axes Theorem is given by the following equation: We introduce a novel method for rectangular selection of components in large 3D models on the web. The moment of inertia of any shape, in respect to an arbitrary, non centroidal axis, can be found if its moment of inertia in respect to a centroidal axis, parallel to the first one, is known.


 0 kommentar(er)
0 kommentar(er)
